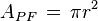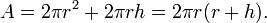GEOMETRİK CİSİMLER NELERDİR?

PİRAMİT:
Bir dik piramidin hacmi, tabanı ve yüksekliği piramidin tabanı ve yüksekliğine eş olan dik prizmanın hacminin üçte birine eşittir.
Piramidin temel elemanları tepe noktası, tabanı, yan yüzleri, ayrıtları ve yüksekliğidir. Piramidin tepe noktasından taban düzlemine inen dikme veya bu dikmenin uzunluğu piramidin yüksekliğidir.
Tepe noktasını taban merkezine (ağırlık merkezine) birleştiren doğru parçası tabana dik ise piramide dik piramit, eğik ise eğik piramit denir. Piramitler, tabanlarını oluşturan çokgensel bölgelere göre üçgen dik pirami, kare eğik piramit vb. şeklinde adlandırılır.
Dik piramitlerin yüzey alanı, taban alanı ile yan yüzlerini oluşturan üçgensel bölgelerin alanları toplanarak bulunur.


KONİ:
Koninin temel elmanları; bir daire olan taban, tabanın dışında bir tepe noktası, tepe noktasını taban merkezine birleştiren doğru parçası olan eksen, tepe noktasından geçen ve tabanın çevresini oluşturan çembere dayanan bir doğrunun süpürdüğü yanal yüzey, bu doğrudan ibaret olan ana doğru (doğuran) 'dur.
Ekseni tabana dik olan koni dik koni (veya dönel koni), eğik olan koni eğik koni olarak adlandırılır.
Dik koninin yanal yüzü, bir dairenin belirli bir merkez açısıyla elde edilen sektörüdür. Koninin tabanı, çevresini uzunluğu bu sektörün yay uzunluğuna eşit olan dairedir.
Dik dairesel koninin yüzey alanı, koninin yanal yüzey alanı ile taban alanı toplanarak bulunur.
Sektörün alanı demek daire diliminin alanı demektir.
Bir dönel koninin düzlemlerle arakesitine, konikler adı verilir. Herhangi bir koni, tabana paralel bir düzlemle kesilirse, düzlemle taban arasında kalan kısma kesik koni denir.



KÜRE:
Kürenin temel elemanları; bir merkez noktası, bu merkez noktasından eşit uzaklıkta bulunan noktaların oluşturduğu yüzey ve yüzeyin herhangi bir noktasını merkeze birleştiren doğru parçası (yarıçap) 'dır.
Özel bir küre, merkezi ve yarıçapı dikkate alınarak hesaplanır.
Merkezden geçen düzlemlerle kürenin ara kesiti olan dairenin çapı aynı zamanda kürenin çapıdır.
Merkezinden geçen düzlemlerle küre yüzeyinin ara kesitine büyük çemberler adı verilir.
Kürenin büyük dairesi, kürenin merkezini içine alan veya merkezinden geçen dairedir. Kürenin yüzey alanı, kürenin en büyük dairesinin alanının 4 katına eşittir.
En büyük çemberin yarıçap uzunluğu r olan bir kürenin hacmi, taban yarıçapı r ve yüksekliği 2r olan dik silindirin hacminin 2/3 üne eşittir.



Formüller
(İki boyutlu, standart) bir küre için kimi formüller:
| Küre formülleri |
| Hacim |
 |
| Projeksiyon Alanı |
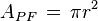 |
| Küre parçasının hacmi |
 |
| Yarıçap |
 |
| Yükseklik |
 |
| Atalet momenti |
 |
SİLİNDİR:
Silindir geometrik bir cisimdir.
- Hacmi:

- Yüzey alanı:
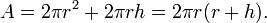
Bir dikdörtgenin bir kenarı etrâfında döndürülmesiyle elde edilir. Bu silindire dik veya eğik silindir denir. Alt ve üst tabanı dâiredir. Soba borusu dik silindire bir örnektir.
Matematikte silindirin genel tanımı şöyledir: Düzlemsel bir eğriyle bu eğrinin düzleminde bulunmayan bir doğru verildiğinde, dâimâ bu doğruya paralel kalmak şartıyla eğriye dayanarak hareket eden bir doğrunun taradığı yüzeye silindirik yüzey denir. Bu silindirik yüzeyle, bu yüzeyi kesen paralel iki düzlemin sınırladığı cisme silindir denir. Silindir yüzeyini meydana getiren doğrulardan herbirine ana doğru denir.
Silindire, taban eğrisine göre isim verilir. Eğri dâireye Şişe dâirevî silindir, elipse ise eliptik silindir denir. Silindirik yüzey için taban eğrisinin kapalı olması gerekmez. Parabolik silindir, hiperbolik silindir, birer silindirik yüzeydir. Dairevî silindirin ana doğrusu tabana dik değilse böyle silindire eğik silindir denir.
Taban yarıçapı “r”, yüksekliği “h” olan bir dik silindirin alan ve hacim formülleri şöyledir:
Yan alan: Y=2πrh
İki taban alanı: 2A=2πr2
Bütün alanı: S=Y+2A=2πrh+2πr2=2πr (h+r)
Hacmi: V= π r2. h
Bayındırlıkta: Bir şasiye monte edilmiş, tekerlek vazîfesi gören bir veya birkaç büyük mâdenî silindirden meydana gelen ve toprağı, şaseleri kaplayan malzemeyi sıkıştırmak ve ezmek için kullanılan, dökme demirden yapılmış büyük ağırlığa, şeklinden dolayı silindir adı verilir.
Otomobilde, tekstil ve kâğıt sanâyiinde çeşitli silindirler kullanılmaktadır.